Sum of Square Roots of First N Numbers in Python

by
4/5 - (1 vote)

There are several methods to calculate the sum of the square roots of the first n numbers.

Basic Iteration

The most straightforward solution is to simply iterate from 1 to n, calculate the square root of each number, and add it to a running total.

import math


def sum_sqrt(n):
    total = 0

    for i in range(1, n+1):
        total += math.sqrt(i)

    return total

print(sum_sqrt(100))

Runtime: O(n)

Approximate Closed Form Solution

An approximate closed-form solution for the sum of square roots from 1 to n is:

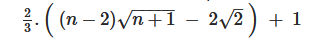
This reduces runtime compared to iteration. However, it is very imprecise for small n and becomes more and more precise for larger n.

def sum_sqrt(n):
    return 2/3 * ((n-2)*(n+1)**0.5-2*2**0.5)+1

Runtime: O(1)

List Comprehension

A list comprehension can calculate all square roots in one line, then sum the results.

def sum_sqrt(n):
    return sum([math.sqrt(i) for i in range(1,n+1)])

print(sum_sqrt(10000))
# 666716.4591971082

Runtime: O(n)

Map/Reduce

Use map to calculate square roots, then reduce to sum results.

from functools import reduce

def sum_sqrt(n):
    total = reduce(lambda a,b: a + b, map(math.sqrt, range(1,n+1)))
    return total

print(sum_sqrt(n))
# 666716.4591971082

Runtime: O(n)

Quick Discussion

All methods provide the same result, but the closed-form solution is most efficient and also the most imprecise with constant runtime O(1), while the others scale linearly O(n) with the number of inputs. Choose based on runtime requirements and code clarity.

Related Tutorials